About Cyclic Pursuit
In order for the TurtleBots to use the cyclic pursuit algorithm, they have to be able to follow a prescribed circle in a robust way. "Global Path Following for the Unicycle and Other Results" by Mohamed I. El-Hawwary and Manfredi Maggiore, provides a robust method for unicycle (TurtleBot) dynamics.
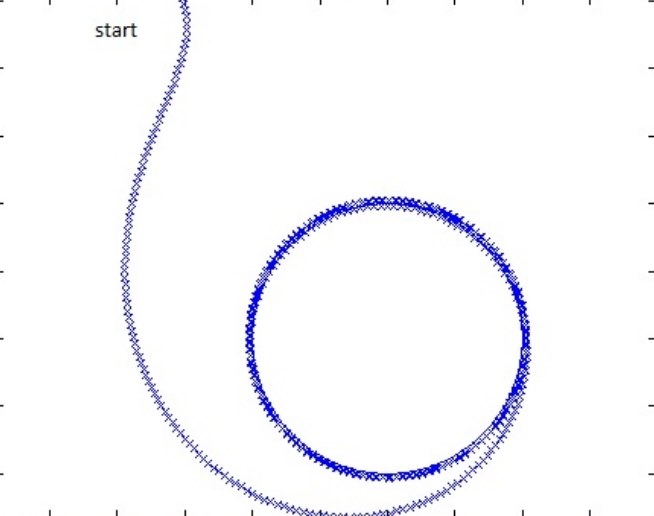
Cyclic Pursuit and Circular Path Following
There are many different kinds of cyclic pursuit algorithms that have been studied. One example of cyclic pursuit is the distribution of moving satellites in a plane around the Earth. The moving satellite would find a stable distance between neighboring satellites through this algorithm. Although there are many versions of cyclic pursuit, we implement a simple model as follows
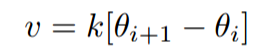
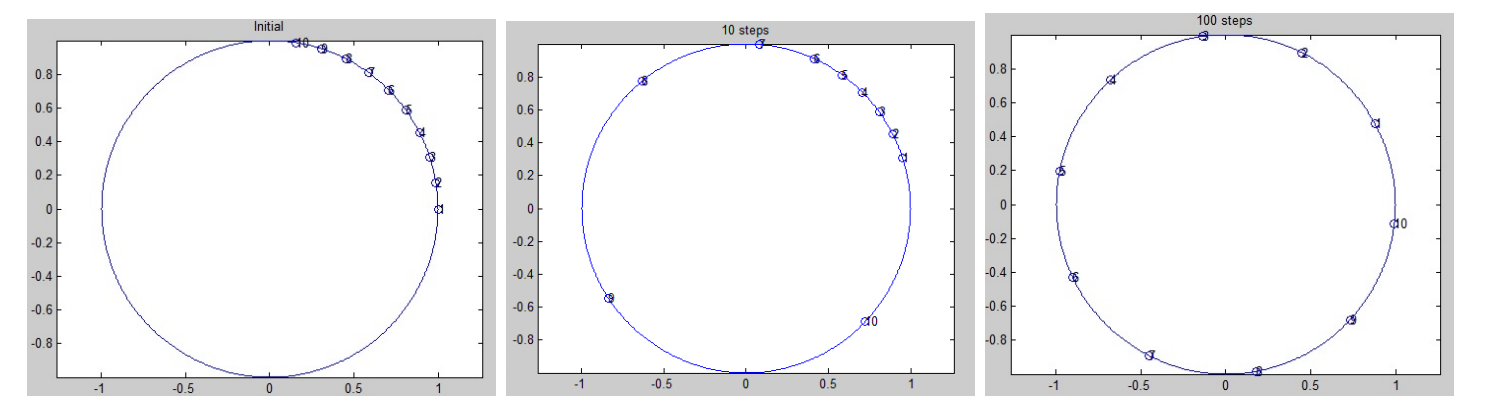
With this algorithm, the turtlebots will reach a steady state (equidistance) equilibrium.
Implementation
In order to run cyclic pursuit, the TurtleBots first had to have the ability to drive in a circle with prescribed speed and radius. We have a couple of options to make this happen such as using a simple pid or sliding mode controller with a goal position. Instead we decided to test an algorithm, “Global Path Following for the Unicycle and Other Results”, by Mohamed I. El-Hawwary, and Manfredi Maggiore[1]. This paper introduces a non-linear controller which drives the TurtleBot to a stable velocity around a prescibed circle origin and radius.
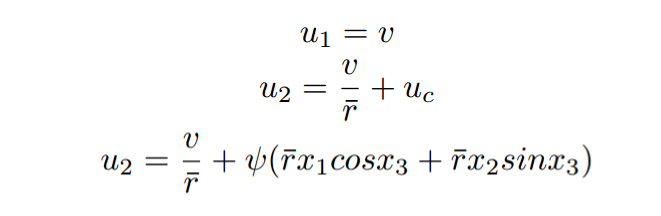
The algorithm needs to know the desired velocity of the TurtleBot. Cyclic pursuit calculates the velocity based on the next TurtleBots distance ahead. Cyclic pursuit tells the circular path following algorithm a low velocity if the TurtleBot is too close to the next Turtlebot, and a high velocity if it is far away. After some time, the TurtleBots (who are all individually running a circular path following algorithm and cyclic pursuit) will reach an equidistant equilibrium.
In ROS
The circular path following algorithm and the cyclic pursuit fits well into the ROS network. The Cyclic pursuit algorithm subscribes to a topic “afterKalman” and “all_positions” to receive the positions of the TurtleBot and it's neighbor. With the position data, cyclic pursuit publishes a velocity based on the previously described algorithm. Circular path following listens to the velocity and influences the TurtleBot to converge to the circle a the desired velocity.
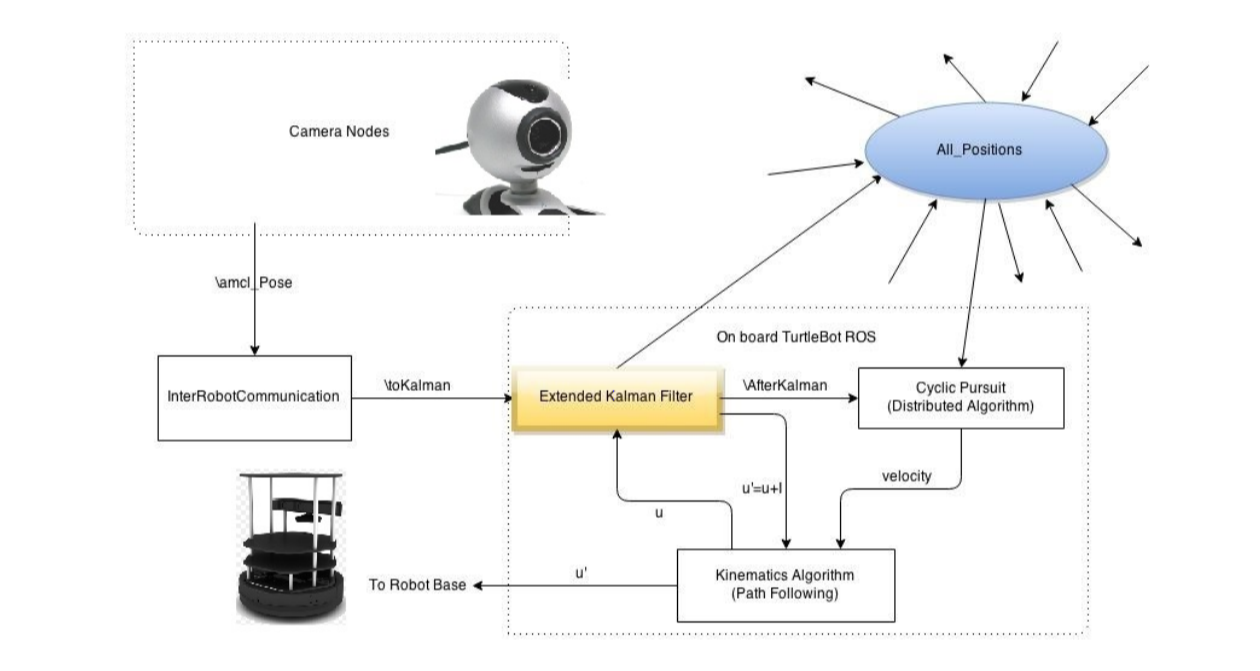
Simulations
Lab Results
Demo of Cicylic Pursuit being implemented on turtleBots.