Hardware Set-Up

Webcam
Localization
The role of the localization subsystem is to provide state estimates of agents to the larger system. In this specific system configuration, a webcam mounted on the ceiling is used to provide a video stream to a computer vision algorithm that finds markers attached to the top of the robots. The node is capable of delivering both location information in the form of Cartesian coordinate and heading information describing the general direction of the robot. Furthermore, the localization scheme is scalable, so that as the number of agents in the network increases, the capability is still supported. no man has gone before.
Computer Vision Algorithms
Aruco Library
In the paper, “Automatic generation and detection of highly reliable fiduciary markers under occlusion”, the authors from Cordoba University outline the robust tracking of markers not dissimilar to QR codes. For practical purposes, there are several benefits for our use of this library, including:
- Black and white are more easily detected in variable lighting environments
- Corner detection is relatively robust
- The ArUco markers have less embedded bits of information than a QR code, making them computationally easier to identify
- The markers contain information, specifically identification numbers
- With knowledge of camera intrinsic, it is possible to extrapolate the orientation of the marker with respect to the camera.
Image of the aruco marker

Edged image after edged texture
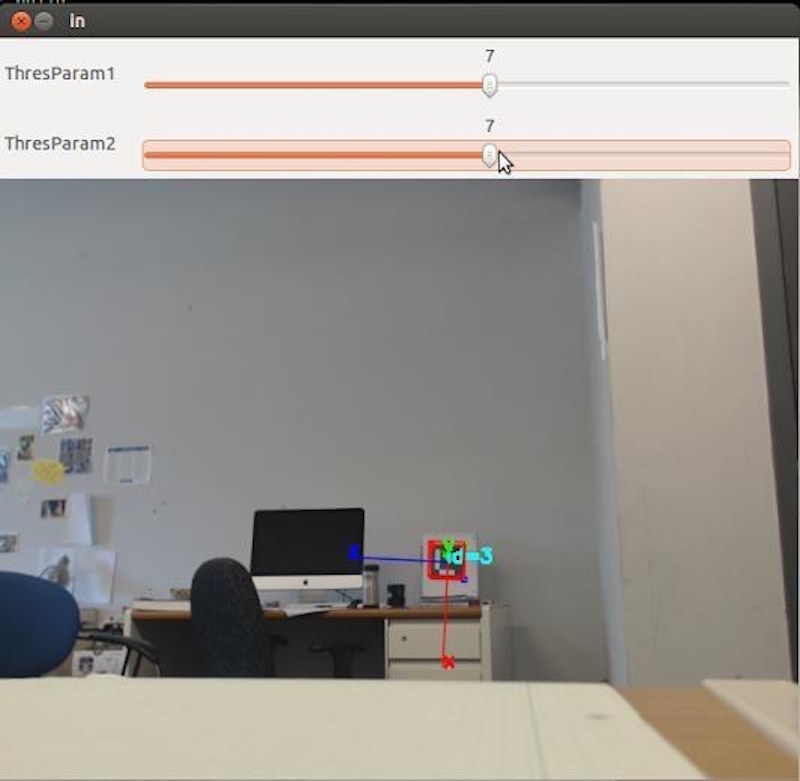
Need to replace this picture with picture of over head camera
The basic workings of the localization code are as follows:
- The image is passed to the processing node
- The image is converted to a OpenCV compatible format
- The ArUco algorithm detects every valid marker
- For each marker that is found, a state information is published on a separate, robot specific topic
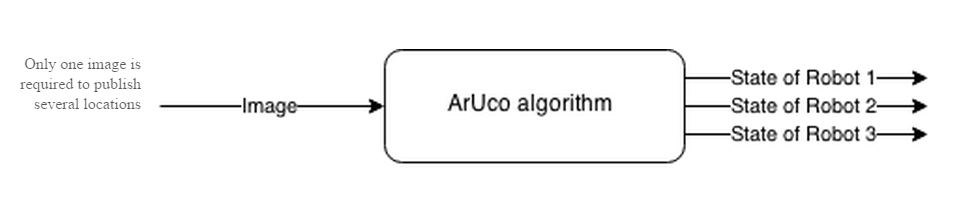
Aruco algorithm flowchart
Extend Kalman Filter (EKF)
Overview
The extended Kalman Filter (EKF) is a powerful tool for state estimation. It is especially important to have strong state estimations for non-linear unicycle (TurtleBot) dynamics where algorithms are highly dependent on consistent data. The Kalman filter works by estimating the state (our TurtleBot locations and orientation), x̂k|k, by fusing measurement data, yk, and a predicted state, x̂k|k-1. The EKF provides several functions for the TurtleBots.
The EKF provides...
1. A state prediction if no measurement data is available.
A common problem with TurtleBots before the EKF, is that the camera's wont always be able to read the TurtleBots location. This is due to many factors including the Aruco markers becoming worn out, the angle of the markers make them more difficult to be detected, or even that the TurtleBots wander outside of the of the camera's visibility. Using the TurtleBots dynamics, the EKF can provide an prediction for where the Turtlebots where be in case there is no measurement data.2. A better estimation
The Kalman filter is created based on the principle that any two data measurements (or predictions) can be merged to yield a better estimate. It requires knowledge of how confident we are in the measurement or prediction that we get (variance). We can always get a better estimate by merging our state prediction and our measurement data for localization of TurtleBots.
3. Provides data for feedback control
After experimenting with the TurtleBots, it is apparent that the dynamics fluctuate due to unknown parameters (could be battery life, part of lab, dust, friction, etc...). The fact that the Turtlebots follow different dynamics under the same inputs make it increasingly difficult to implement distributed algorithms. One way to deal with this is to implement integral control. Integral control sums the error over time and modifies the input signal. It is commonly used to fix steady state error between the estimated state and the reference. The Kalman filter makes this possible by providing an state prediction, and an estimated state (fusion of state prediction and measured data). Forcing the difference between the predicted state and the estimated state to be gaussian by modifying our input forces the TurtleBots to follow a reference signal in a more predictable fashion.
Theory
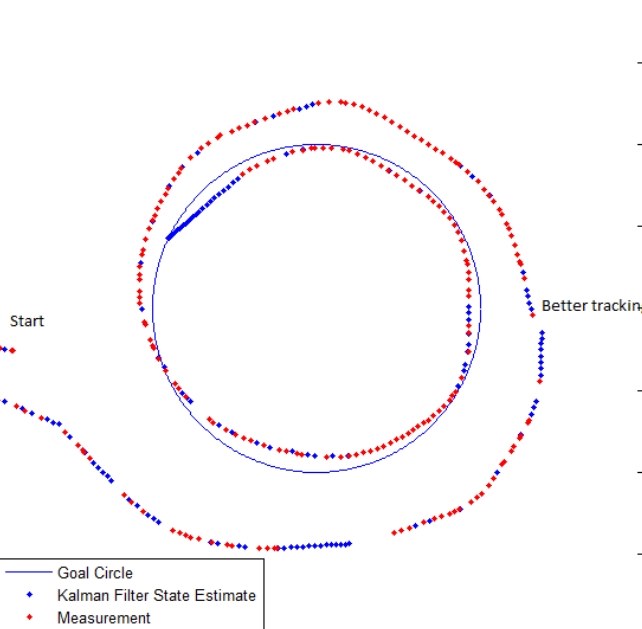
Every once in a while, the measurements from the camera are not available. Here are the best estimated locations of a TurtleBot based on state prediction and measurement data as it follows a circle. Red Dots are best estimates when measurements are available. Blue Dots are best estimates when no measurement is available (predicted state)
Implementation
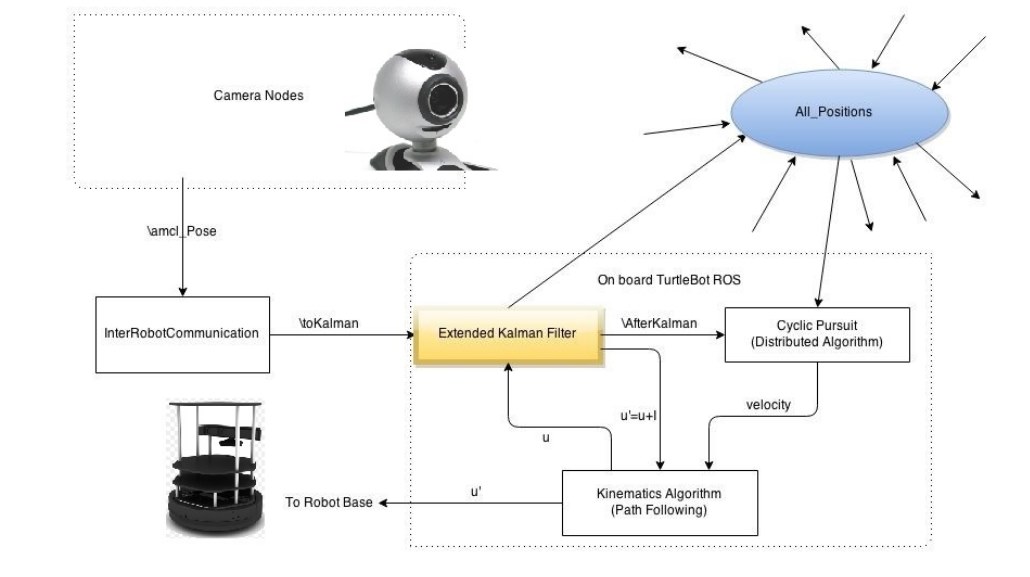 1. Camera node detects and publishes robot positions
2. Node distributes and identifies robot positions
3. Kalman filter calculates best estimated position
4a. Best estimated position sent to application
4b. Integral variable sent to application
1. Camera node detects and publishes robot positions
2. Node distributes and identifies robot positions
3. Kalman filter calculates best estimated position
4a. Best estimated position sent to application
4b. Integral variable sent to application